The Squaring of the Circle, part I. and part II.
© E.S. 2016 first edition, 2019 second edition.

I. The squaring of the circle and its purpose

From another perspective:
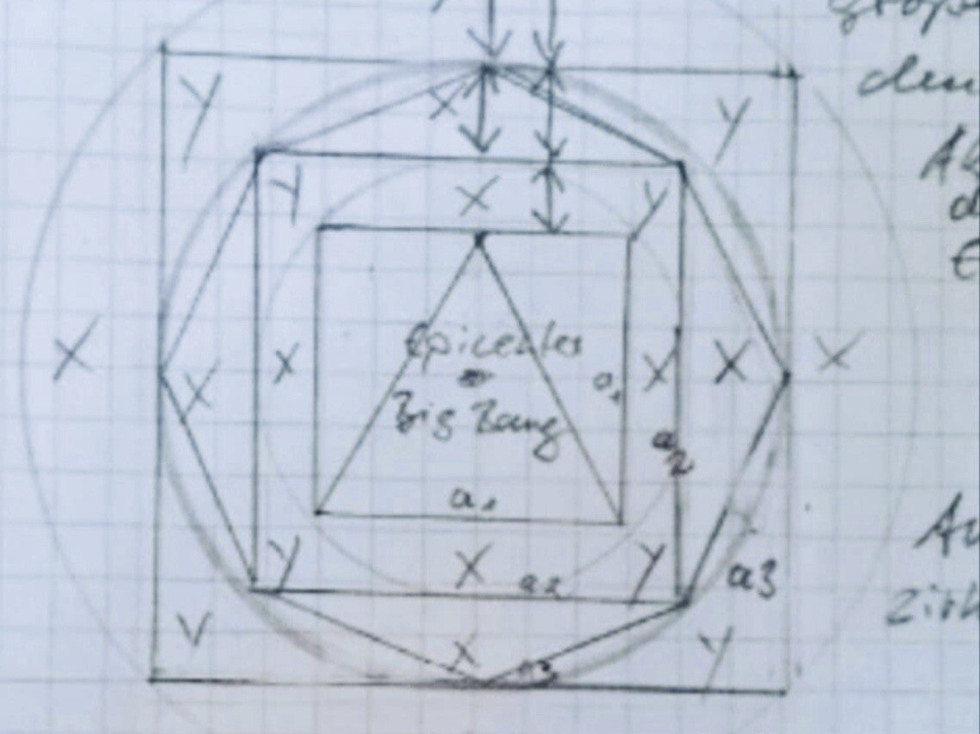
When dimensioned as shown in the graph (first graph), proportionally increasing distances are definable, e.g. distances of (micro)waves, expansion of the universe (due to the Big Bang), circular wave extensions caused by earthquakes, i.e. circular extensions, as with a stone, which is thrown into a pond, circular waves are being formed relatively proportionally.

Description of the mathematical process:
The square is considered the basis of the calculation, because the squaring as 'terminus technicus' cannot be transferred to other geometrical figures, like e.g. on the triangle, since there is no "triangling".

a = π × r ^ 2
π × r ^ 2 - a ^ 2 = x
a ^ 2 - π × r ^ 2 = y

[x + a ^ 2 = area of the circle
y + π × r ^ 2 = area of the square]

x + a ^ 2 ≙ π × r ^ 2

Conclusion:
a (1) ^ 2 ≙ a (2) ^ 2 - y ≙ a (3) ^ 2 + x ≙ a (4) ^ 2 - y = ∞

II. The squaring of the circle

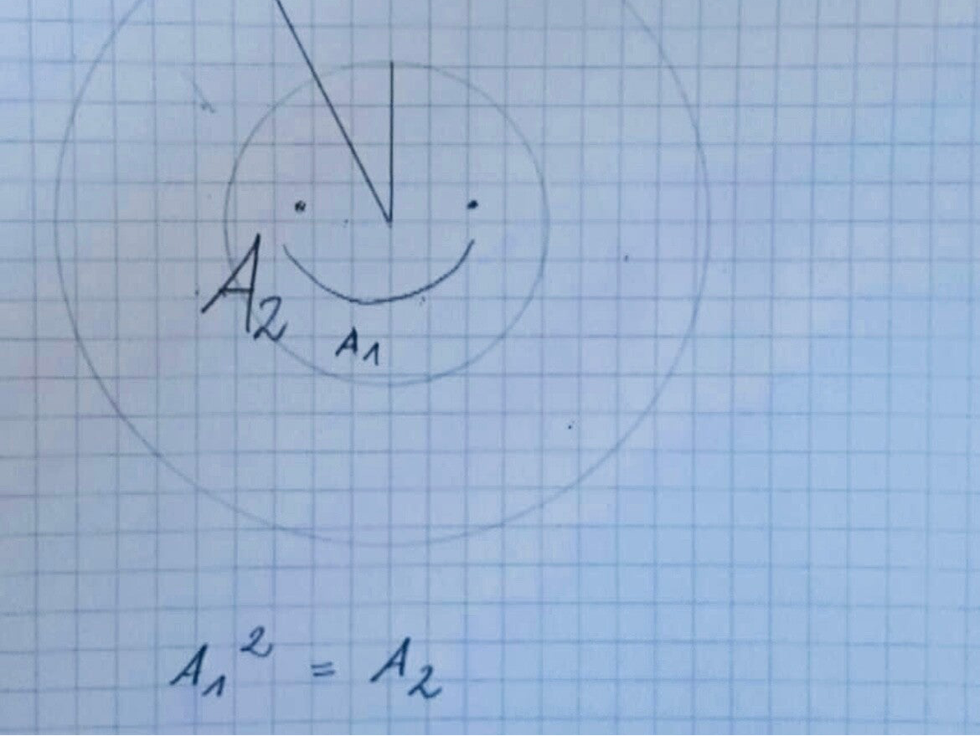
seen this way (second graph):
A1 ^ 2 = A2

Full explanation in text:

In the first part of "The Squaring of the Circle" the purpose and mathematical process behind this concept is dicussed. The squaring of the circle refers to finding a square with the same area as a given circle.

From another perspective, when we dimension the circle as shown in the graph, we can define proportionally increasing distances. This can be seen in various phenomena such as the expansion of the universe, circular wave extensions caused by earthquakes, or even the circular waves formed when a stone is thrown into a pond.

The mathematical process involves considering the square as the basis of the calculation because the squaring operation cannot be applied to other geometrical figures like triangles. We use the formula a = π × r^2, where "a" represents the area of the circle. By subtracting the square of "a" from π × r^2, we get the value of "x." Similarly, by subtracting π × r^2 from the square of "a," we obtain the value of "y."

The conclusion drawn is that a (1)^2 is equivalent to a (2)^2 - y, which is equivalent to a (3)^2 + x, and so on, resulting in an infinite sequence.

It should be noted that the values for x must be greater than 1 (x > 1) in order for the calculation to work. If the values are less than x, the calculation will not work. This means that in this case, the calculation would only work if values below 1 were used, which would need to be interpreted computationally as values above 1, similar to values above one when squaring. This contradicts, here, the rule of calculation for squaring values <1 in terms of practical effect. This is a new insight.

Moving on to the second part, the squaring of the circle can be seen differently, second graph. Here, A1^2 is equal to A2.

ℹ️ 

The mathematical derivation for calculating the area of a circle is based on the well-known value of Pi (π). Pi is a mathematical constant that describes the ratio of a circle's circumference to its diameter. Historically, the first approximation of Pi originated in ancient Egypt, but it was mathematical developments by Archimedes and later by Isaac Newton and Gottfried Leibniz that led to a more accurate calculation.

To calculate the area of a circle, we use the formula A = π x r^2, where A represents the area and r is the radius of the circle. The radius is the distance from the center of the circle to any point on its edge.

The derivation of this formula is based on integration in calculus. One simple method involves dividing the circle into a large number of very thin rings. Each ring has a width of Δr and an area of 2πr x Δr. By summing the areas of the rings and letting the limit of Δr approach zero, we obtain the exact formula for the area.

Historically, mathematicians like Archimedes used this method to approximate the area of a circle. They approximated the circle using regular polygons, such as hexagons, and calculated the area of these polygons. The more sides the polygon had, the more accurate the approximation for the circle's area.

James Stuart, Calculus, Early Transcendentals, Brooks Edition 8, 2015.

Further information:

https://www.mathopenref.com/circleareaderive.html